あらすじ
前回は集合論のイントロダクションで、高校時の「集合と論理」の集合の復習と+αを学んだ。
(詳しくは集合論 イントロダクション)
今回は論理のところを復習していく。
命題
正しいか正しくないかが明確である文章や式を命題という。
集合を定める時もそうだが、数学の明瞭さや正しさを担保するために明確であるということを
ものすごく大切にしている。
この明確であるという部分は判断ができるという意味で決して正しいとは限らない。
例えばサルは亀である。という文章は間違っているが正しいか正しくないかは明確なので命題だ。
このとき、正しいことを真といい、正しくないことを偽という。
集合との関係
Pが正しいとき、Qも正しいということをPならばQであるという。(記号\(P\Rightarrow Q\))
例えば、九州に住んでいるならば日本で住んでいるといった感じだ。
このことは集合の考え方と結びつけることができる。
前回集合の表し方として外延的記法というものを学んだ。
Pを満たしているものを全て集めた集合は外延的記法を用いて
\(\{x|P(x)\}\)とかけるのであった。
同様にQの条件を満たしているものを全て集めた集合は\(\{x|Q(x)\}\)とかける。
さて、\(P \Rightarrow Q\)を集合としてみた場合、Pを満たしている要素はQの要素でもあるので、
\(\{x|P(x)\} \subset \{x|Q(x)\}\)とかける。
余談だが、私は外延的記法は集合と命題の関係を繋ぐための架け橋のようなものだと捉えている。
対偶の真偽
\(P \Rightarrow Q\)が正しいかどうかは\(\{x|P(x)\}\)の要素は\(\{x|Q(x)\}\)となるかを判定する以外でないのか。
その他の一つの方法が対偶を確認するという方法である。
対偶とは元の命題\(P \Rightarrow Q\)に対して、QでないならばPでないという命題のことだ。
この対偶を示す、すなわち\(\{x|Q(x)\}^{c} \subset \{x|P(x)\}^{c}\)を示すことだ。
なぜこれを示せば良いのかを以下で説明する。
対偶と元の命題の真偽が一致する理由
まずは、直観的に理解する。
\(P \Rightarrow Q\)が成り立つということは\(\{x|P(x)\} \subset \{x|Q(x)\}\)である.
ベン図を書くと、このようになる。
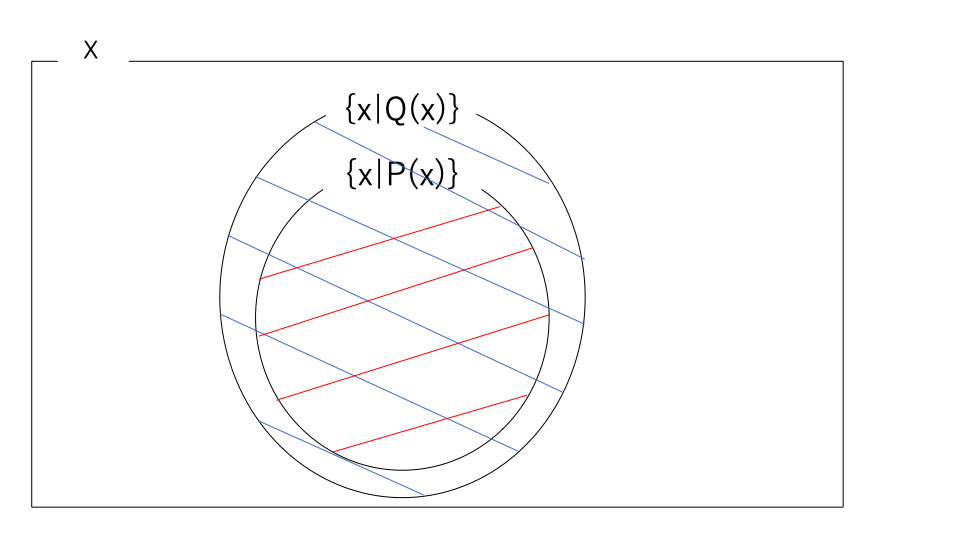
青い部分が赤い部分を含んでいることがわかる。
そして見方を変えて、外側を見てみる。
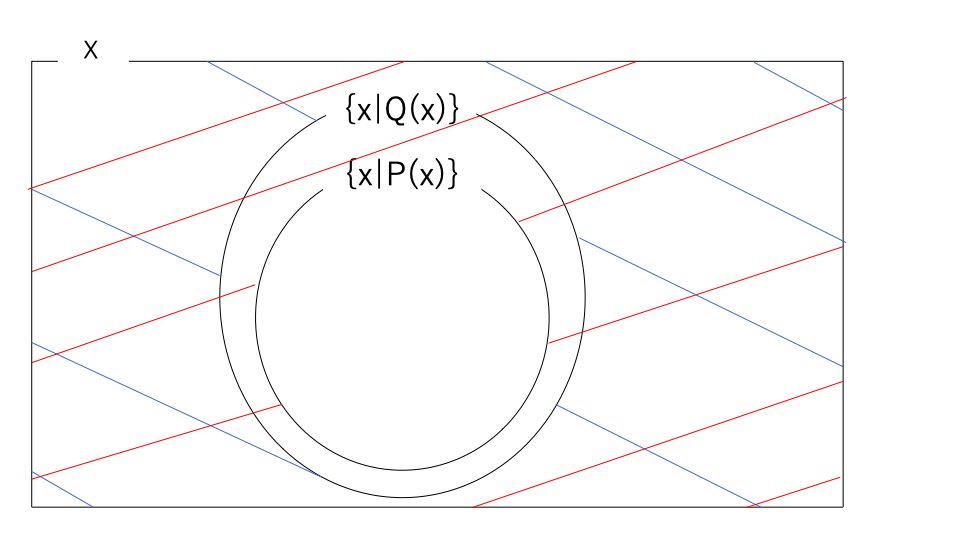
今度は、赤い部分が青い部分を含んでいることが発見できる。
これは、すなわち\(\{x|Q(x)\}^{c} \subset \{x|P(x)\}^{c}\)となっている。
これが直観的な理解である。次に定義に従って論理的に証明する。
対偶と元の命題の真偽が一致する証明
\(\{x|P(x)\} \subset \{x|Q(x)\} \)を仮定して、\(\{x|Q(x)\}^{c} \subset \{x|P(x)\}^{c}\)を示す。
集合の包含関係を示すにはどうしたらいいかは、定義に戻れば良い。
集合A,BについてAから好きにとってきたaがどれもBの要素でもあった時、
AはBの部分集合であるという。(記号:\(A \subset B\))
このとき、AはBに含まれるという。
これより、\(\{x|Q(x)\}^{c}\)から好きに要素をとってきて、その要素が\(\{x|P(x)\}^{c}\)に属することを示す.
\(\{x|Q(x)\}^{c}\)から好きに要素aをとる.
補集合の定義より,\(a \notin \{x|Q(x)\}\)となる.
ここで,\(a \in \{x|P(x)\} \Leftrightarrow a \notin \{x|P(x)\}\)より、\(a \notin \{x|P(x)\}\)を示せば終了となる.
これを背理法で示す.\(a \in \{x|P(x)\} \)を仮定する.
\(\{x|P(x)\} \subset \{x|Q(x)\} \)であるから,\(a \in \{x|Q(x)\}\)となる.
しかしこれは,\(a \notin \{x|Q(x)\}\)に矛盾する.
従って,aは\(\{x|P(x)\}^{c}\)に属する.
\(\)
コメント